STA 517 3.0 Programming and Statistical Computing with R
Lesson 3: Functions in R
Dr Thiyanga Talagala
2020-08-30
Functions in R
👉🏻 Perform a specific task according to a set of instructions.
Functions in R
👉🏻 Perform a specific task according to a set of instructions.
👉🏻 Some functions we have discussed so far,
c,matrix,array,list,data.frame,str,dim,length,nrow,plot
Functions in R
👉🏻 Perform a specific task according to a set of instructions.
👉🏻 Some functions we have discussed so far,
c,matrix,array,list,data.frame,str,dim,length,nrow,plot
👉🏻 In R, functions are objects of class function.
class(length)[1] "function"Functions in R
👉🏻 Perform a specific task according to a set of instructions.
👉🏻 Some functions we have discussed so far,
c,matrix,array,list,data.frame,str,dim,length,nrow,plot
👉🏻 In R, functions are objects of class function.
class(length)[1] "function"👉🏻 There are basically two types of functions:
💻 Built-in functions
Already created or defined in the programming framework to make our work easier.👨 User-defined functions
Sometimes we need to create our own functions for a specific purpose.Basic components of a function
Syntax
name <- function(arg1, aug2, ...){<FUNCTION BODY>return(value)}Example
cal_sqrt <- function(x){a <- x^2b <- x^3out <- c(a, b)names(out) <- c("squared", "cubed")out # or return(out)}Evaluation
cal_sqrt(2)squared cubed 4 8Basic components of a function
Syntax
name <- function(arg1, aug2, ...){<FUNCTION BODY>return(value)}Example
cal_sqrt <- function(x){a <- x^2b <- x^3out <- c(a, b)names(out) <- c("squared", "cubed")out # or return(out)}Evaluation
cal_sqrt(2)squared cubed 4 8👉 Functions are created using the function().
Basic components of a function
Syntax
name <- function(arg1, aug2, ...){<FUNCTION BODY>return(value)}Example
cal_sqrt <- function(x){a <- x^2b <- x^3out <- c(a, b)names(out) <- c("squared", "cubed")out # or return(out)}Function name: cal_sqrt
use verbs, where possible.
should be meaningful.
Use an underscore (_) to separate words.
avoid names of built-in functions.
start with lower case letters. Note that R is a case sensitive language.
Basic components of a function
Syntax
name <- function(arg1, aug2, ...){<FUNCTION BODY>return(value)}Example
cal_sqrt <- function(x){ a <- x^2 b <- x^3 out <- c(a, b) names(out) <- c("squared", "cubed") out # or return(out)}Function arguments: x
- value passed to the function to obtain the function's result.
Basic components of a function
Syntax
name <- function(arg1, aug2, ...){<FUNCTION BODY>return(value)}Example
cal_sqrt <- function(x){ a <- x^2 b <- x^3 out <- c(a, b) names(out) <- c("squared", "cubed") out # or return(out)}Function body
Function body (Cont.)
Place spaces around all operators such as =, +, -, <-, etc.
Exception: Do not place spaces around the operators :, :: and :::
1+2 # bad1 + 2 # goodFunction body (Cont.)
Place spaces around all operators such as =, +, -, <-, etc.
Exception: Do not place spaces around the operators :, :: and :::
1+2 # bad1 + 2 # good- Place a space before left parentheses except evaluating the function (function call)
if (a > 2) # goodif(a>2) # bad# Function call ----rnorm(2) # goodrnorm (2) # bad- Use extra spacing to align multiple lines with <- or =
# Bad ------a = sum(c(1, 5, 8, 10))/2sd = sd(c(1, 5, 8, 10))# Good ------a = sum(c(1, 5, 8, 10))/2sd = sd(c(1, 5, 8, 10))Function body (Cont.)
- Spacing inside parentheses or square brackets
# Good ---a[1, 2]a[1, ]if(x < 2)# Bad ---a[1,2]a[1,]if(x<2)if( x<2 )- {} do not go in one single line, always two lines
# Good ---if(y == 2){print("even")}# Bad ---if(y == 2){ print("even")}Built-in Functions
How to call a built-in function in R
function_name(arg1 = 1, arg2 = 3)Argument matching
The following calls to mean are all equivalent
mydata <- c(rnorm(20), 100000)mean(mydata) # matched by positionmean(x = mydata) # matched by namemean(mydata, na.rm = FALSE)mean(x = mydata, na.rm = FALSE) mean(na.rm = FALSE, x = mydata) mean(na.rm = FALSE, mydata)[1] 4761.693⚠️ Even though it works, do not change the order of the arguments too much.
Argument matching (cont.)
- some arguments have default values
mean(mydata, trim=0)[1] 4761.693mean(mydata) # Default value for trim is 0[1] 4761.693mean(mydata, trim=0.1)[1] -0.1329687mean(mydata, tr=0.1) # Partial Matching[1] -0.1329687?mean
Your turn
- Calculate the mean of 1, 2, 3, 8, 10, 20, 56, NA.
Basic maths functions
| Operator | Description |
|---|---|
| abs(x) | absolute value of x |
| log(x, base = y) | logarithm of x with base y; if base is not specified, returns the natural logarithm |
| exp(x) | exponential of x |
| sqrt(x) | square root of x |
| factorial(x) | factorial of x |
Basic statistic functions
| Operator | Description |
|---|---|
| mean(x) | mean of x |
| median(x) | median of x |
| mode(x) | mode of x |
| var(x) | variance of x |
| sd(x) | standard deviation of x |
| scale(x) | z-score of x |
| quantile(x) | quantiles of x |
| summary(x) | summary of x: mean, minimum, maximum, etc. |
Type conversion functions
| Test | Convert |
|---|---|
| is.numeric() | as.numeric() |
| is.character() | as.character() |
| is.vector() | as.vector() |
| is.matrix() | as.matrix() |
| is.data.frame() | as.data.frame() |
| is.factor() | as.factor() |
| is.logical() | as.logical() |
| is.na() |
Type conversion functions
| Test | Convert |
|---|---|
| is.numeric() | as.numeric() |
| is.character() | as.character() |
| is.vector() | as.vector() |
| is.matrix() | as.matrix() |
| is.data.frame() | as.data.frame() |
| is.factor() | as.factor() |
| is.logical() | as.logical() |
| is.na() |
Example
a <- c(1, 2, 3); a[1] 1 2 3is.numeric(a)[1] TRUEis.vector(a)[1] TRUEb <- as.character(a); b[1] "1" "2" "3"is.vector(b)[1] TRUEis.character(b)[1] TRUEYour turn
Remove missing values in the following vector
[1] 0.61940020 -0.93808729 0.95518590 -0.22663938 0.29591186 NA [7] 0.36788089 0.71791098 0.71202022 0.22765782 NA NA[13] -0.74024324 0.02081516 -0.14979979 -0.22351308 0.98729725 NA[19] NA NA NA NA NA NA[25] NA NA NA -1.50016003 0.18682734 0.20808590[31] 0.70102264 -0.10633074 -1.18460046 0.06475501 0.11568817 -0.04333140[37] -0.22020064 0.02764713 0.10165760 -0.18234246 1.32914659 -1.29704248[43] 1.05317749 -0.70109051 0.09798707 0.10457263 -0.21449845Probability distribution functions
Each probability distribution in R is associated with four functions.
Naming convention for the four functions:
For each function there is a root name. For example, the root name for the normal distribution is
norm. This root is prefixed by one of the lettersd,p,q,r.d prefix for the distribution function
p prefix for the cumulative probability
q prefix for the quantile
r prefix for the random number generator
Example:
dnorm,pnorm,qnorm,rnorm
Illustration with Standard normal distribution
The general formula for the probability density function of the normal distribution with mean μ and variance σ is given by
fX(x)=1σ√(2π)e−(x−μ)2/2σ2
If we let the mean μ=0 and the standard deviation σ=1, we get the probability density function for the standard normal distribution.
fX(x)=1√(2π)e−(x)2/2
Standard Normal Distribution
fX(x)=1√(2π)e−(x)2/2
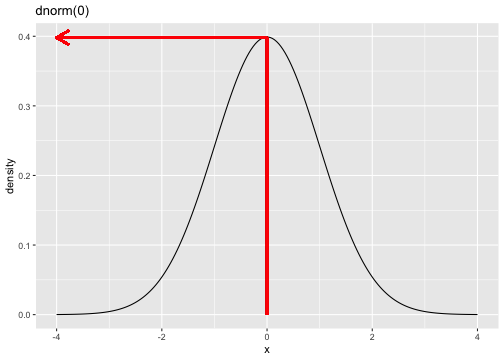
dnorm(0)[1] 0.3989423Standard Normal Distribution
fX(x)=1√(2π)e−(x)2/2
pnorm(0)[1] 0.5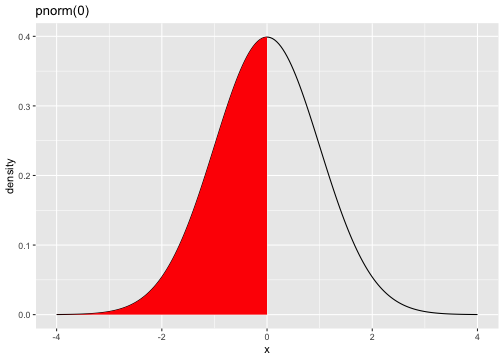
Standard Normal Distribution
fX(x)=1√(2π)e−(x)2/2
pnorm(0)[1] 0.5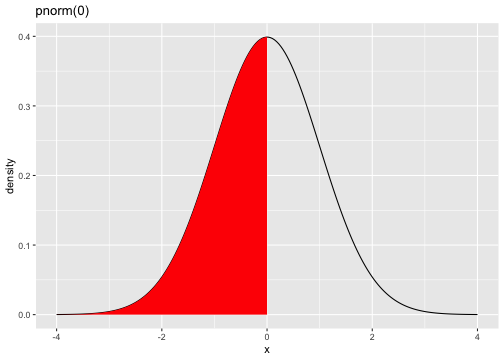
Standard Normal Distribution
fX(x)=1√(2π)e−(x)2/2
qnorm(0.5)[1] 0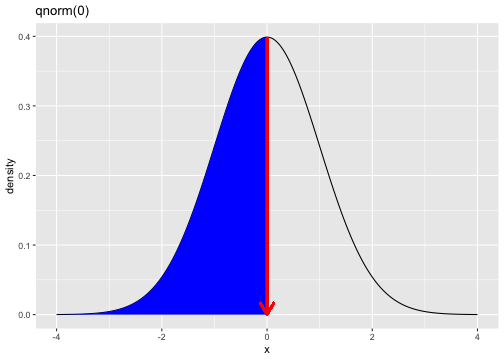
Standard Normal Distribution: rnorm
set.seed(262020)random_numbers <- rnorm(10)random_numbers [1] 0.20078181 0.95873346 1.18369056 1.49513750 1.18109222 -0.57789570 [7] 0.01790671 0.81185245 0.39488199 -0.44337927sort(random_numbers) ## sort the numbers then it is easy to map with the graph [1] -0.57789570 -0.44337927 0.01790671 0.20078181 0.39488199 0.81185245 [7] 0.95873346 1.18109222 1.18369056 1.49513750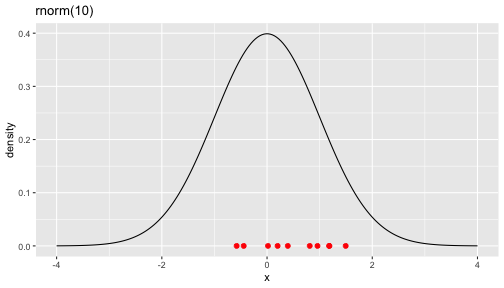
Other distributions in R
beta: beta distributionbinom: binomial distributioncauchy: Cauchy distributionchisq: chi-squared distributionexp: exponential distributionf: F distributiongamma: gamma distributiongeom: geometric distributionhyper: hyper-geometric distribution
lnorm: log-normal distributionmultinom: multinomial distributionnbinom: negative binomial distributionnorm: normal distributionpois: Poisson distributiont: Student's t distributionunif: uniform distributionweibull: Weibull distribution
Other distributions in R
beta: beta distributionbinom: binomial distributioncauchy: Cauchy distributionchisq: chi-squared distributionexp: exponential distributionf: F distributiongamma: gamma distributiongeom: geometric distributionhyper: hyper-geometric distribution
lnorm: log-normal distributionmultinom: multinomial distributionnbinom: negative binomial distributionnorm: normal distributionpois: Poisson distributiont: Student's t distributionunif: uniform distributionweibull: Weibull distribution
🙋 Getting help with R:
?Distributions
Your turn
Suppose Z∼N(0,1). Calculate the following standard normal probabilities.
P(Z≤1.25),
P(Z>1.25),
P(Z≤−1.25),
P(−.38≤Z≤1.25).
Find the following percentiles for the standard normal distribution.
90th,
95th,
97.5th,
Determine the Zα for the following
α=0.1
α=0.95
Suppose X∼N(15,9). Calculate the following probabilities
P(X≤15),
P(X<15),
P(X≥10).
A particular mobile phone number is used to receive both voice messages and text messages. Suppose 20% of the messages involve text messages, and consider a sample of 15 messages. What is the probability that
At most 8 of the messages involve a text message?
Exactly 8 of the messages involve a text message.
Generate 20 random values from a Poisson distribution with mean 10 and calculate the mean. Compare your answer with your friend's answer.
Reproducibility of scientific results
rnorm(10) # first attempt [1] 1.4701904 -0.2375662 0.1765985 -0.5257483 -1.3674764 -1.4422500 [7] 0.7576607 0.6475122 -1.1543034 0.9066248rnorm(10) # second attempt [1] -1.7603264 -0.3402939 -1.0335807 1.0645014 -0.3874459 0.5975271 [7] -2.1535707 0.6602928 1.1581404 0.6133446As you can see above you will get different results
set.seed(1)rnorm(10) # First attempt with set.seed [1] -0.6264538 0.1836433 -0.8356286 1.5952808 0.3295078 -0.8204684 [7] 0.4874291 0.7383247 0.5757814 -0.3053884set.seed(1)rnorm(10) # Second attempt with set.seed [1] -0.6264538 0.1836433 -0.8356286 1.5952808 0.3295078 -0.8204684 [7] 0.4874291 0.7383247 0.5757814 -0.3053884R Apply family and its variants
apply()function
marks <- data.frame(maths=c(10, 20, 30), chemistry=c(100, NA, 60))marks maths chemistry1 10 1002 20 NA3 30 60apply(marks, 1, mean)[1] 55 NA 45apply(marks, 2, mean) maths chemistry 20 NAR Apply family and its variants
apply()function
marks <- data.frame(maths=c(10, 20, 30), chemistry=c(100, NA, 60))marks maths chemistry1 10 1002 20 NA3 30 60apply(marks, 1, mean)[1] 55 NA 45apply(marks, 2, mean) maths chemistry 20 NAapply(marks, 1, mean, na.rm=TRUE)[1] 55 20 45Your turn
Calculate the row and column wise standard deviation of the following matrix
[,1] [,2] [,3] [,4][1,] 1 6 11 16[2,] 2 7 12 17[3,] 3 8 13 18[4,] 4 9 14 19[5,] 5 10 15 20Your turn
Assignment 1: Individual
Find about the following variants of apply family functions in R lapply(), sapply(), vapply(), mapply(), rapply(), and tapply() functions.
Resourses: You can follow the DataCamp tutorial here.
You should clearly explain,
syntax for each function
function inputs
how each function works?/ The task of the function.
output of the function.
differences between the functions (apply vs lapply, apply vs sapply, etc.)
Provide your own example for each function.
Use only 1 A4 sheet, you may use both sides.
Assignment due date: 6 September 2020
Example: lapply()
lapply(x, FUN)
input: vector or list
output: list of the same length as input
task: apply FUN function to all elements in the input
lapply(list(c(1, 2, 3), c(10, 20, 30)), mean)[[1]][1] 2[[2]][1] 20lapply(c(10, 20, 30), mean)[[1]][1] 10[[2]][1] 20[[3]][1] 30Data Visualization: qplot()
?qplot
Data Visualization: qplot()
?qplot

Installing R Packages
Method 1
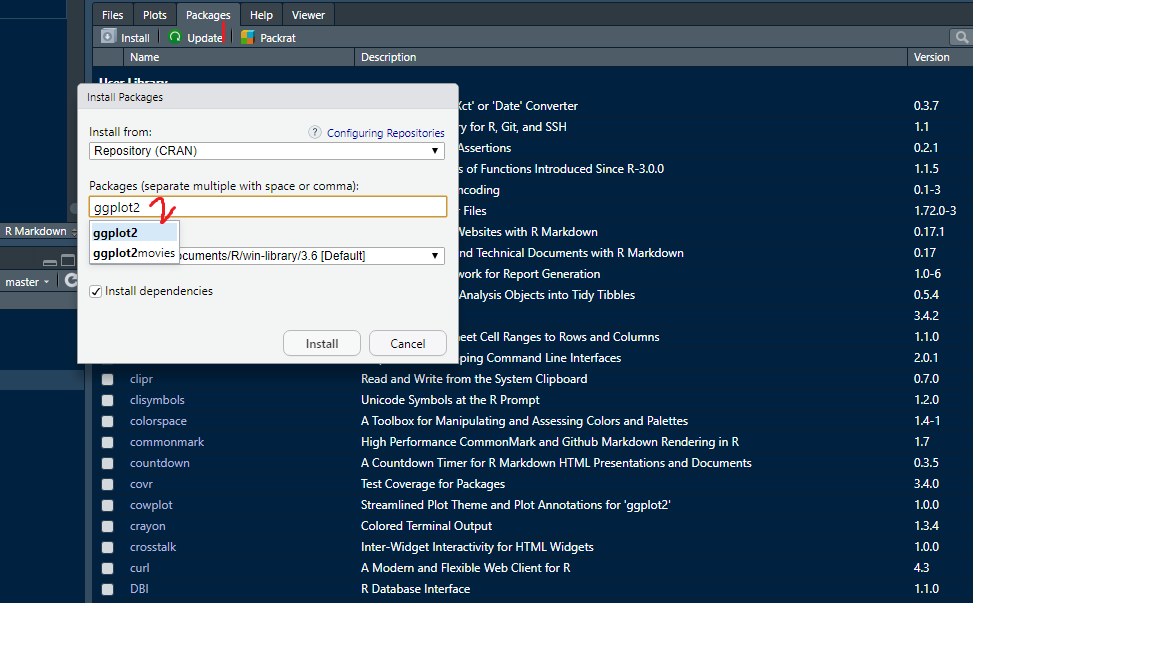
Method 2
install.packages("ggplot2")Load package
library(ggplot2)Now search ?qplot
Note: You shouldn't have to re-install packages each time you open R. However, you do need to load the packages you want to use in that session via library.
mozzie dataset
library(mozzie)data(mozzie)Data Visualization with qplot
plot vs qplot
plot(mozzie$Colombo, mozzie$Gampaha)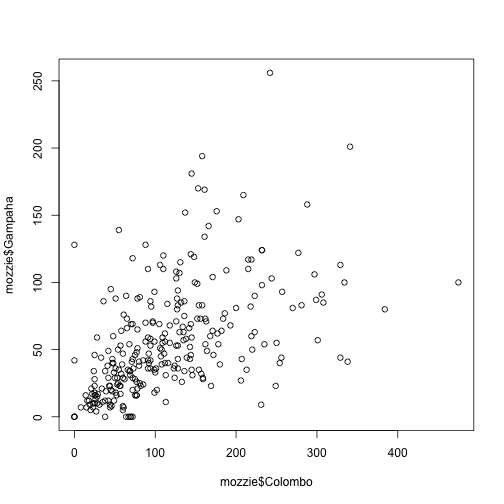
qplot(Colombo, Gampaha, data=mozzie)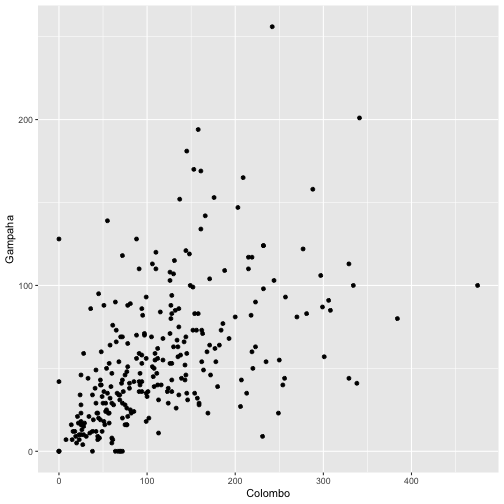
Data Visualization with qplot
qplot(Colombo, Gampaha, data=mozzie)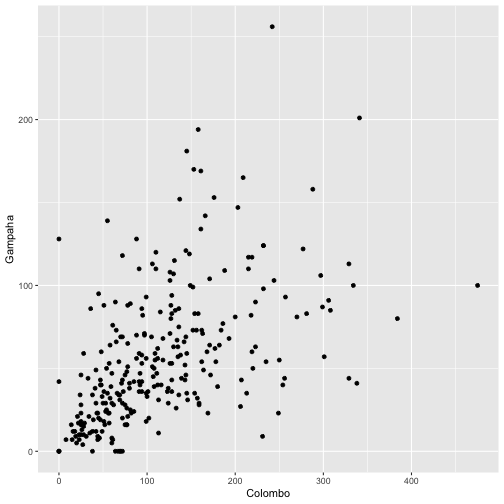
qplot(Colombo, Gampaha, data=mozzie, colour=Year)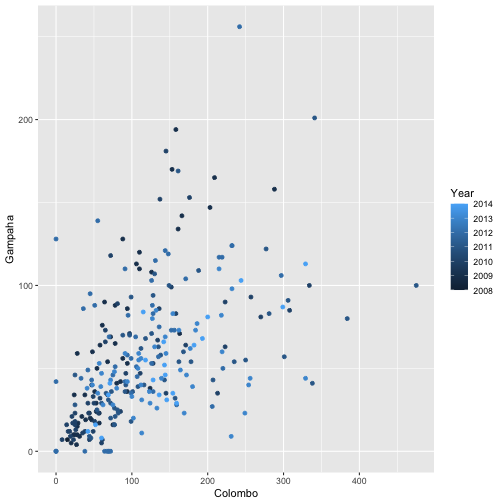
Data Visualization with qplot
qplot(Colombo, Gampaha, data=mozzie)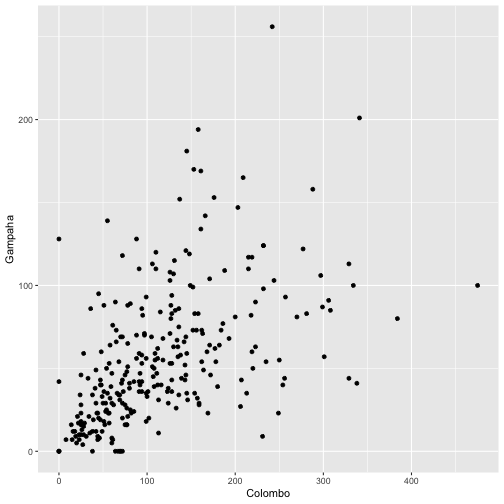
qplot(Colombo, Gampaha, data=mozzie, size=Year)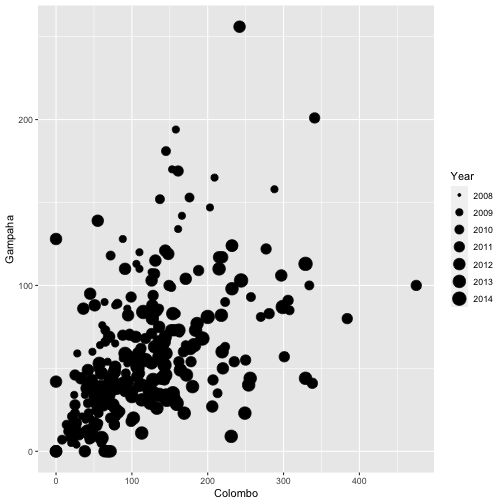
Data Visualization with qplot
qplot(Colombo, Gampaha, data=mozzie)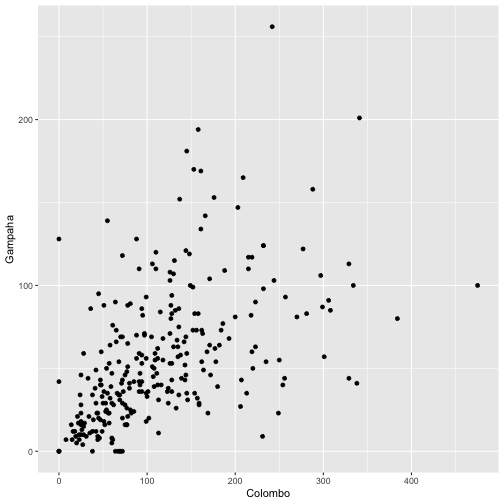
qplot(Colombo, Gampaha, data=mozzie, geom="point")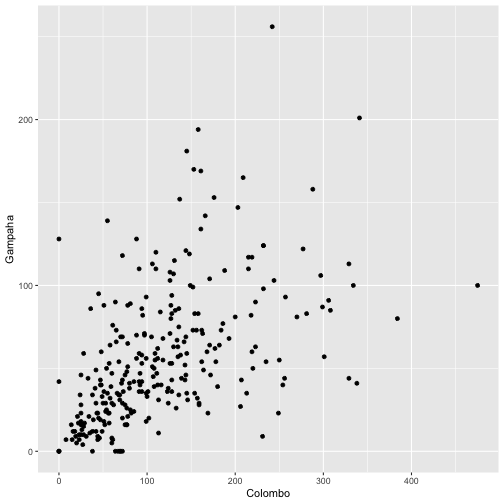
Data Visualization with qplot
qplot(ID, Gampaha, data=mozzie)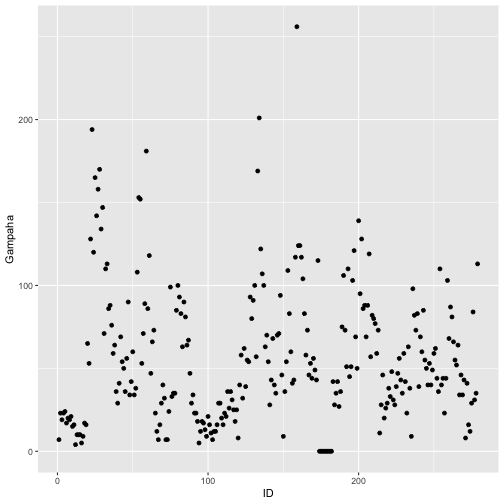
qplot(ID, Gampaha, data=mozzie, geom="line")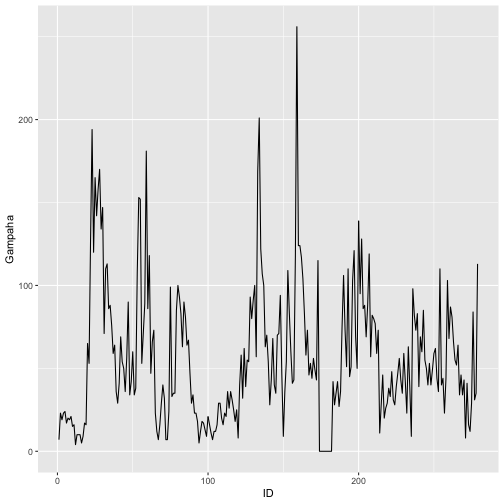
Data Visualization with qplot
qplot(ID, Gampaha, data=mozzie)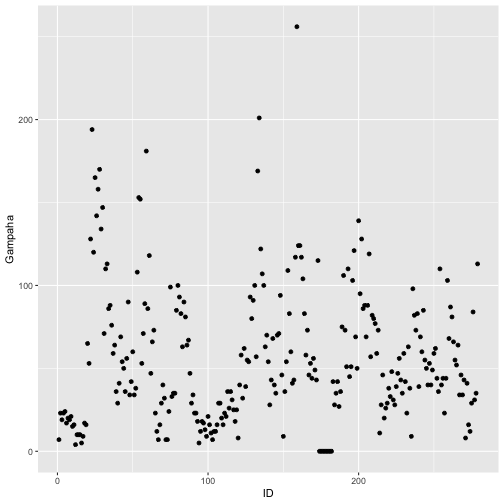
qplot(ID, Gampaha, data=mozzie, geom="path")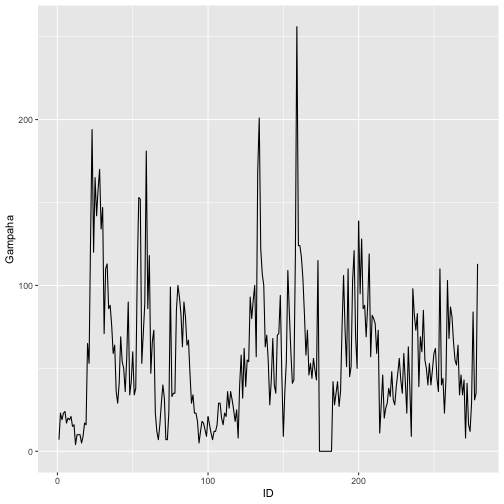
Data Visualization with qplot
qplot(Colombo, Gampaha, data=mozzie, geom="line")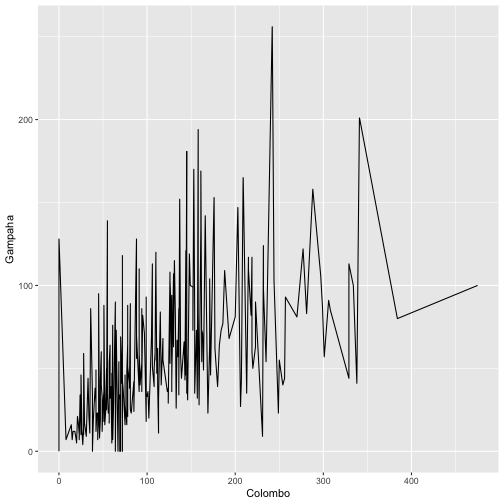
qplot(Colombo, Gampaha, data=mozzie, geom="path")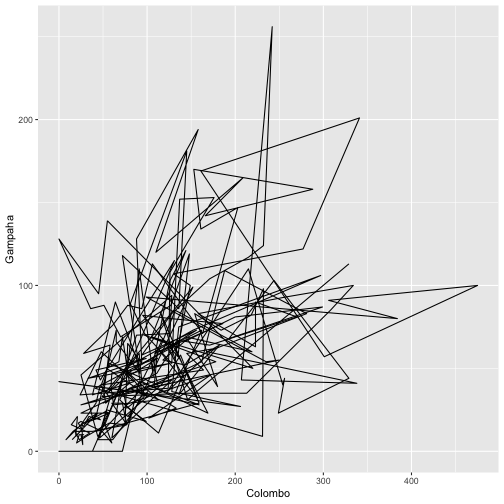
Data Visualization with qplot
qplot(Colombo, Gampaha, data=mozzie, geom=c("line", "point"))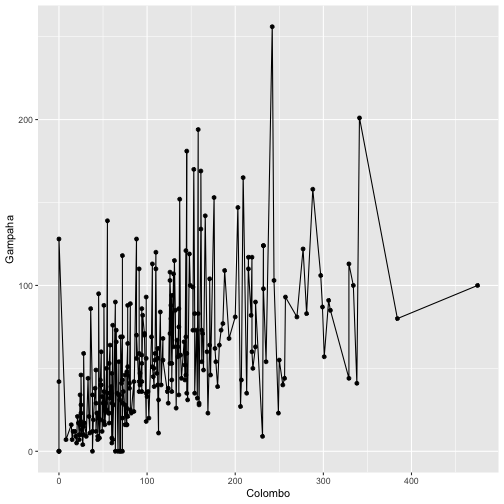
qplot(Colombo, Gampaha, data=mozzie, geom=c("path", "point"))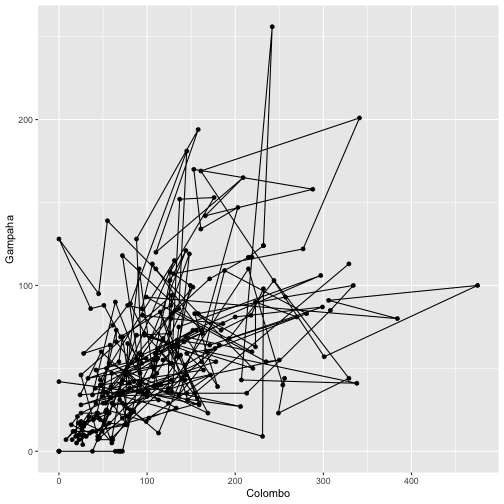
Data Visualization with qplot
boxplot(Colombo~Year, data=mozzie)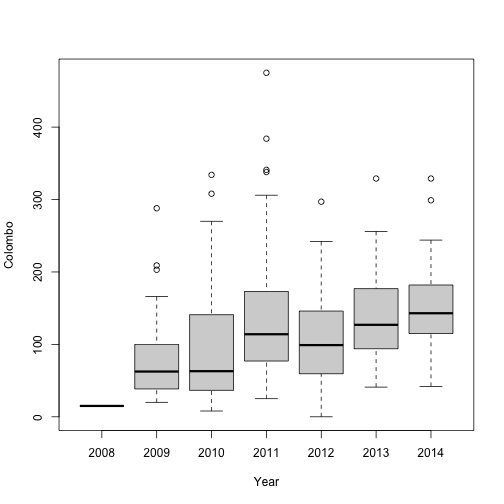
qplot(factor(Year), Colombo, data=mozzie, geom="boxplot")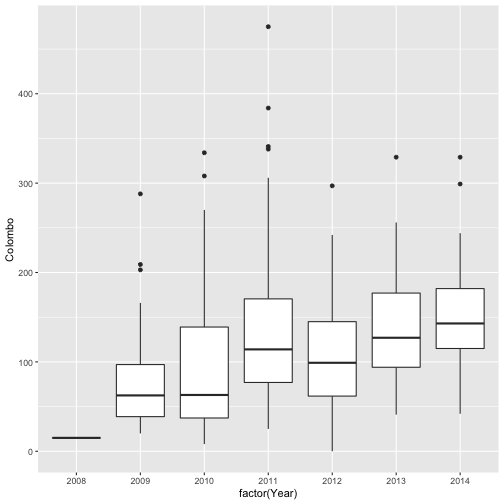
Data Visualization with qplot
qplot(factor(Year), Colombo, data=mozzie, geom="boxplot")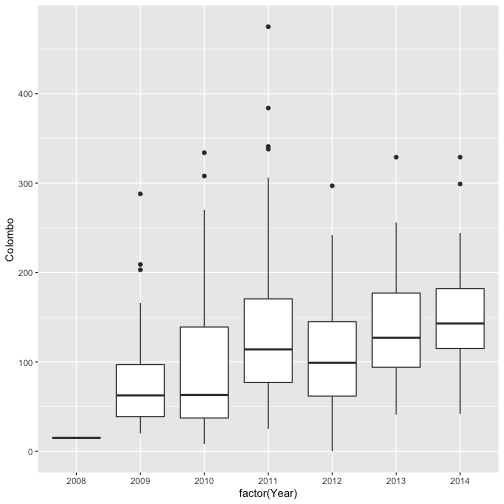
qplot(factor(Year), Colombo, data=mozzie) # geom="point"-default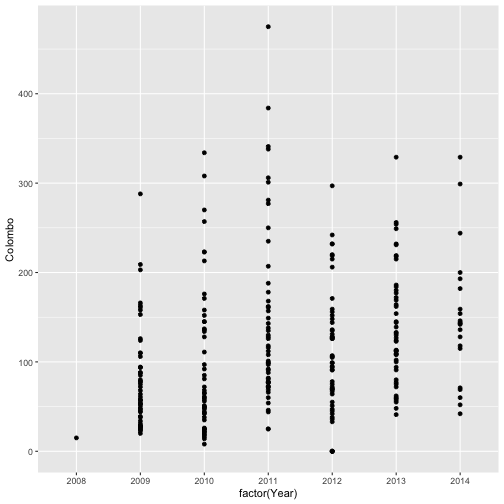
Data Visualization with qplot
qplot(factor(Year), Colombo, data=mozzie, geom="point")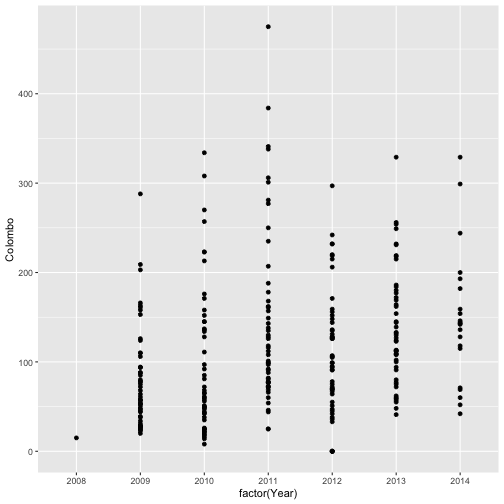
qplot(factor(Year), Colombo, data=mozzie, geom=c("jitter", "point")) # geom="point"-default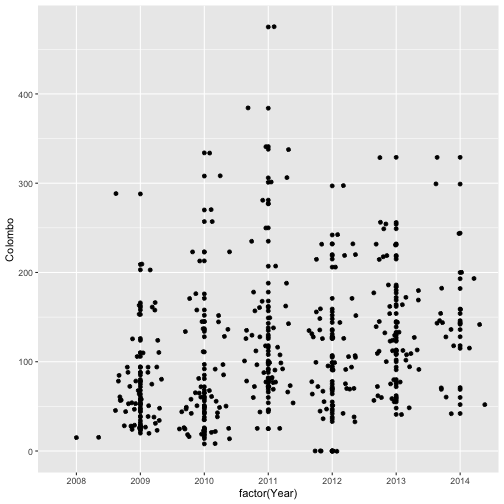
Data Visualization with qplot
qplot(factor(Year), Colombo, data=mozzie, geom=c("jitter", "point"))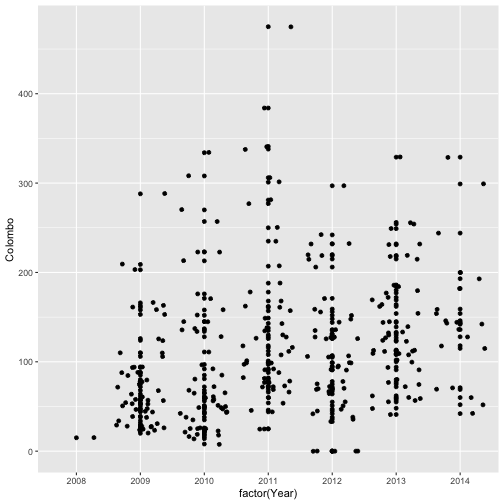
qplot(factor(Year), Colombo, data=mozzie, geom=c("jitter", "point", "boxplot")) # geom="point"-default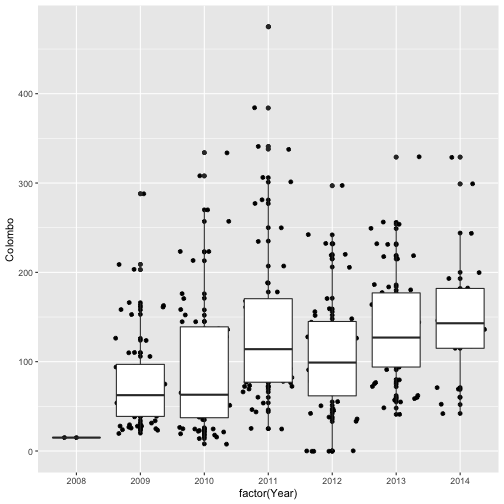
Data Visualization with qplot
qplot(Colombo, data=mozzie)`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.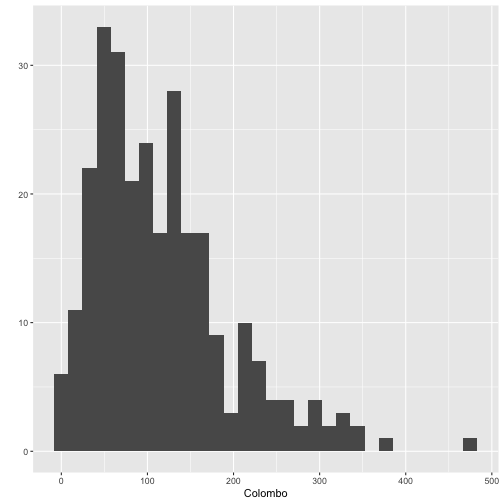
qplot(Colombo, data=mozzie, geom="density")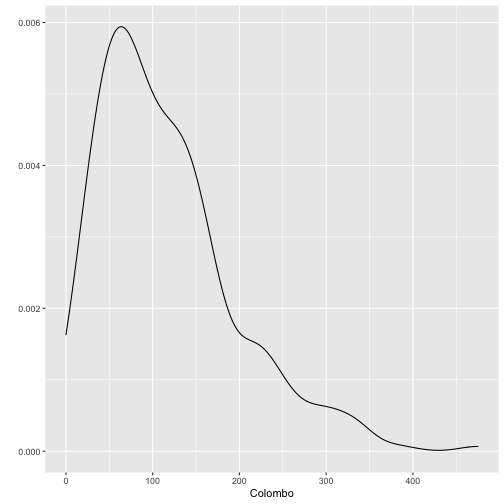
Your turn
Explore iris dataset with suitable graphics.
head(iris) Sepal.Length Sepal.Width Petal.Length Petal.Width Species1 5.1 3.5 1.4 0.2 setosa2 4.9 3.0 1.4 0.2 setosa3 4.7 3.2 1.3 0.2 setosa4 4.6 3.1 1.5 0.2 setosa5 5.0 3.6 1.4 0.2 setosa6 5.4 3.9 1.7 0.4 setosa
Slides available at: https://thiyanga.netlify.app/courses/rmsc2020/contentr/
All rights reserved by Thiyanga S. Talagala